|
<< Click to Display Table of Contents >> Array ohmic wiring loss |
  
|
|
<< Click to Display Table of Contents >> Array ohmic wiring loss |
  
|
Definition
The ohmic resistance of the wiring circuit induces losses ( ELoss = Rw · I² ) between the power available from the modules and the power at the terminals of the sub-array.
The relevant parameter for the simulation is the Rw value, which is an equivalent resistance of the wires, as "seen" from the input of the global sub-array (i.e. the set of MPPT inputs defined in this sub-array). You should define one Rw value for each sub-array in your system.
First stage evaluation: percentage of STC
The Rw value evaluation will highly depend on the sub-array structure.
However PVsyst provides a convenient way of defining a default value to be used during the first stages of the study of a PV system.
We specify a Power loss ratio with respect to the STC power.
We can consider the equivalent "resistance" of the STC operating point: RarraySTC = Vmp / Imp (at STC) [ohm].
Then the Wiring loss fraction = Rw / RarraySTC (ratio, or percentage).
In PVsyst we have chosen a default initial value of 1.5% (at STC) for this usual loss. This default may be modified in the Hidden parameters ("Default Wiring Resistance loss ratio at STC") for the initialization of any new project/variant.
Loss in the simulation
The ohmic losses behave in a quadratic way with the array current: Ploss = Rw · Iarray².
Now if the array is not operating at STC, the wiring loss fraction will become:
Ploss / Parray = Rw * Iarray² / (Varray * Iarray) = Rw * Iarray / Varray.
i.e. proportional to Iarray. This means that at half the irradiance (half the current), the wiring loss fraction will be half, etc. Therefore the Wiring energy loss has to be evaluated at each hour of the simulation, and accumulated in terms of energy.
The final result of the Ohmic wiring loss (in terms of percentage) as shown on the loss diagram will be from this hourly energy balance. It is usually of the order of 60% of the Loss fraction specified a STC.
Final calculation: evaluating the resistance
In the latest stages of the project, the equivalent wiring resistance should normally be calculated according to the real lengths and sections of the installed wires.
The program offers a special tool intended to optimise the wire diameters at each stage of the array.
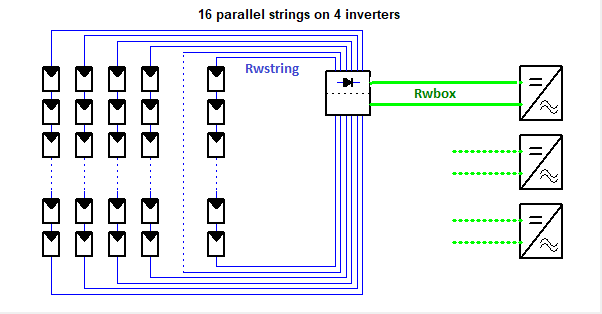
Combining Strings to a junction box
| We try to evaluate the equivalent resistance | Rstrbox of N strings at the input of a junction box. |
| The currents in each string are identical: | Istring = Ibox / Nstr |
| We define the total wires resistance | Rwirestot = Sum(wires lengths) [m] * Resistivity[ohm/m] |
| and an average resistance of each string | Rwstring = Rwirestot / Nstr |
Now the total Power loss of these circuits will be the sum of the unit power losses: Ploss = Rwirestot * Istring² = Rwstring * Nstr * Istring² = Rwstring / Nstr * Ibox²
| Finally we can identify | Rstrbox = Rwstring / Nstr |
Therefore the equivalent resistance of all strings in parallel is the average of the resistivity of each string, divided by the number of strings.
Be careful: this calculation - based on energy loss - is valid whatever the differences in length of the different strings. The equivalent resistance is not the resistances of each individual string calculated as parallel resistances.
Combining Junction boxes to the Sub-array (inverters) input
If all the junction boxes are identical (same number of strings), we can apply exactly the same calculation to the circuits between the junction boxes and the inverter's inputs:
If we define Rwbox as the average resistance of the wires from one box to the inverter input (sum of the 2 wires):
| Circuit wires resistance for several boxes | RwArray = Rwbox / Nbox |
| Now our final result, i.e. the total contribution of the strings + box connection resistances, will be the sum |
| Rw = R (total array) = (RstrBox + Rwbox) / Nbox |
| Restrictions: | this calculation is valid for identical boxes, i.e. same number of strings on each junction box (but with possible different wire lengths). |
If the differences are not too important, this calculation remains quite satisfactory, as it applies to a wiring loss correction of the order of 1% of the yield (second order uncertainties). A rigorous calculation would involve taking the different currents in each junction box into account.
Adding stages: eventual combination boxes
You can add additional stages (junction boxes gathered on combination boxes) by using the same techniques. This is namely available in the optimization tool.
Voltage drop
Many engineers usually think about ohmic loss in terms of a voltage drop.
This cannot be defined with a PV array, as on the I/V curve the current is closely related to the voltage. When choosing the Pmpp, diminishing the Voltage increases the current.
Therefore we can only define the Wiring loss in terms of Power loss.
Calculation
There are two ways of evaluating the wires ohmic Power loss:
| - | If we only need the MPP power, we can directly define the loss Pw(loss) = Rw * Impp². |
| - | If we need some other operating point on the I/V curve, we have to recalculate the I/V curve from the one-diode model, by adding the Rw to the Rserie of the PV modules. |
We have checked that the results of both methods are very close to each other.