Power Factor

Summary

In an AC circuit, power (or energy, when integrated over time) can be described by three main components:

Active Power: This is the real power that performs useful work—such as generating movement or heat. It is measured in [kW], which are also sometimes written [kWac] in the specific context of discussing power factor.
Reactive Power: A form of "virtual" power, created or absorbed by components like inductors (e.g., motors) or capacitors. It does not result in any net energy transfer. It is measured in [kVAr].
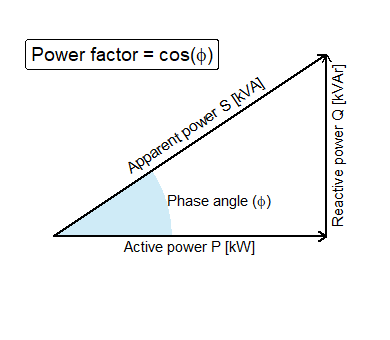
Apparent Power: The vectorial combination of active and reactive power components. It is measured in [kVA].

In sinusoidal systems, these power contributions result from the phase shift between the current and the voltage waveforms. The so-called power factor defines the ratio of active to apparent power as $$ PF = \cos(\phi) $$

As well as converting photovoltaic output into active AC power, inverters can supply or absorb reactive energy. Grid operators may therefore request that PV systems supply reactive power to compensate for the reactive loads elsewhere on the network (motors, switched-mode power supplies, etc.).

Basic definitions



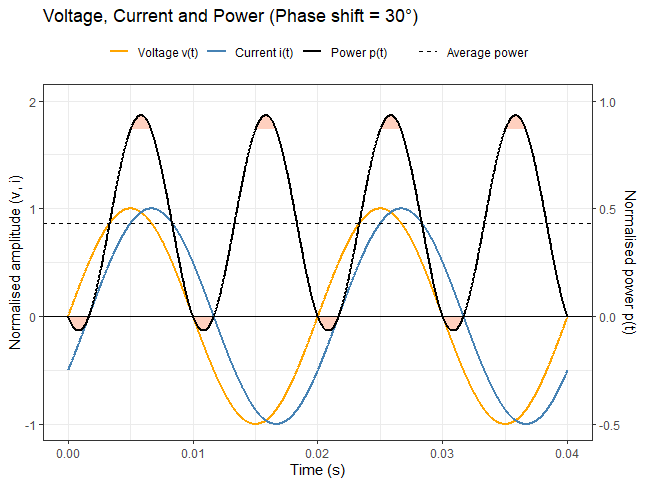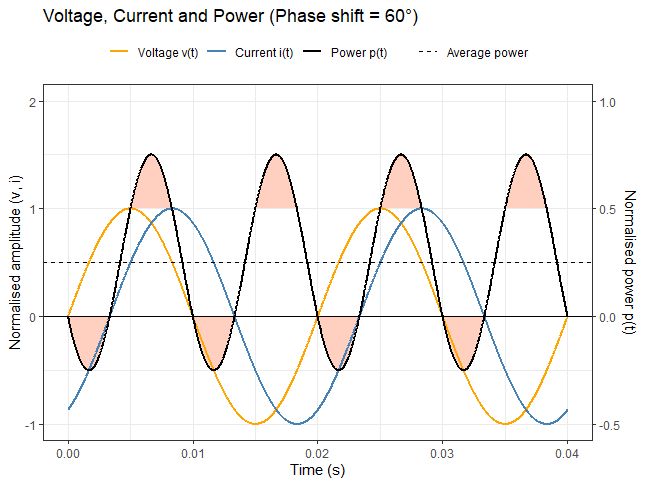Instantaneous current, voltage and power with a phase shift of 30°	Instantaneous current, voltage and power with a phase shift of 60°.

In an AC circuit, current and voltage are time-varying waveforms. For a single angular frequency $\omega=2\pi f$ the instantaneous current and voltage can be written

\[ \begin{align} i(t) &= \sqrt{2}I_{RMS}\cos(\omega t), \\ v(t) &= \sqrt{2}V_{RMS}\cos(\omega t + \phi), \end{align} \]

where the RMS value of a periodic signal is $x_{RMS} \doteq \sqrt{\frac{1}{T}\int_{0}^{T}x^2(t)dt }$.

The phase difference between current and voltage $\phi$ is positive when the current is lagging behind the voltage and negative when the current is leading in front of the voltage.

The instantaneous power is the product of the instantaneous voltage and current which reads

\[ \begin{align} p(t) &\doteq v(t)i(t) \\ &= V_{RMS}I_{RMS}\cos(\omega t + \phi)\cos(\omega t) \\ &= \underbrace{V_{RMS}I_{RMS}\cos(\phi)}_{\text{DC component}} \\ &+ \underbrace{V_{RMS}I_{RMS}\cos(2\omega t + \phi)}_{\text{AC component}}, \end{align} \]

where we used some trigonometric formula in the last equality. The first term is time-independent (a “DC” term), whereas the second oscillates at $2\omega$.

The average (real / active) power over one period is

\[ \begin{align} P &\doteq \frac{1}{T}\int_{0}^{T}p(t)dt \\ & = V_{RMS}I_{RMS}\cos(\phi) \\ & + V_{RMS}I_{RMS}\underbrace{\frac{1}{2\pi}\int_{0}^{2\pi} \cos(2\omega t + \phi)}_{=0} \\ & = V_{RMS}I_{RMS}\cos(\phi) \end{align} \]

where we note that the integral of the AC term over a full cycle is zero. Hence only the DC component transmits usable energy; the AC component alternates sign and transfers no net power.

A phase shift $\phi$ therefore reduces the transferable power. This motivates defining the power factor (PF) as a measure of transmission efficiency:

\[ PF \doteq \frac{P}{V_{RMS}I_{RMS}} \]

Note that in the case of more comple waveforms, this definition of the power factor still applies. For our simple sinusoid we recover the familiar relationship

\[ PF = \cos(\phi). \]

Apparent, reactive and active power definition

The previous time-domain derivation is intuitive but becomes tedious for arbitrary cases. Using phasors notation (complex number) is more convenient. In this framework, the waveforms are extended to the complex domain via Euler’s formula

\[ \begin{align} \check{i}(t) &= I_{RMS}\exp^{i\omega t}\\ \check{v}(t) &= V_{RMS}\exp^{i\omega t + i\phi}. \end{align} \]

Note that the normalisation factor $\sqrt{2}$ disappears to keep the correct value of the RMS signal, which for complex waveforms is defined as $x_{RMS} \doteq \sqrt{\frac{1}{T}\int_{0}^{T}x(t)x^*(t)dt }$, with $x^*(t)$ the complex conjugate of $x(t)$.

The so-called apparent power S is defined as

\[ \begin{align} S &\doteq \check{v}(t) \check{i}^*(t) \\ &= V_{RMS}I_{RMS} \exp^{i\phi} \\ &= V_{RMS}I_{RMS} \cos(\phi) + i V_{RMS}I_{RMS} \sin(\phi). \end{align} \]

This quantity is constant in time and is directly equal to its time averaged. (Note the use of the complexe conjugate of the curent $\check{i}^*(t)$ in that definition: having used $\check{i}(t)$ instead would result in a quantity whose time averaged is zero and therefore would not have been very useful).

The real part of the apparent power is labeled as the active power P, which is the same as in the previous derivation,

\[ P \doteq V_{RMS}I_{RMS} \cos(\phi) \]

and its imaginary part is labeled as the reactive power Q $$ Q = V_{RMS}I_{RMS} \sin(\phi). $$

As we have seen in the time-domain explanation, only the active power delievers useful power and is crucial to understand that the reactive power cannot be used to produce movement, heat, or any tangible energy output. Conversely, reactive power can be generated without consuming any active power—this is the case with capacitors and inductors.

The relationship between apparent energy, reactive energy and active energy is therefore $$ S = P + iQ $$ often visualised as the right-triangle “power diagram”:

Within this framework the power factor is simply $$ PF \doteq \frac{P}{||S||} = \cos(\phi). $$ again measuring how effectively the apparent power translates into real, useful power.

Units in PVsyst

S, P and Q are all measureable quantities of a pair of signals $i(t)$ and $v(t)$. Electric utilities define rules that can apply either on active, reactive or apparent power. Despite all these quantities having units of power, pseudo-units are used in practice to differentiate their role in transmitting power. In PVsyst, they are naturally related to the apparent, reactive and active energy delivered to the grid (integrating those powers over time), for which we give the notation in the following table

Quantity	Units	Related Quantity in PVsyst	Units
Apparent Power S	[kVA]	Apparent Energy transfered to the grid EApGrid	[kVAh]
Reactive Power Q	[kVAr]	Reactive Energy transfered to the grid EReGrid	[kVARh]
Active Power P	[kW], also sometimes [kWac]	Active energy transfered to the Grid E_Grid	[kWh]

Reactive power produced by an inverter

The active energy produced by an inverter always originates from the input DC energy supplied by the PV array. Any real energy difference between the inverter’s input and output is converted into heat, representing the inverter's inefficiency.

With modern technologies such as Pulse Width Modulation (PWM), it is now possible to generate voltage and current signals with any desired phase shift—without any additional energy cost. Traditionally, this compensation is handled using large banks of capacitors. The ability to generate such a phase shift is the result of explicit control within the inverter, defined by a parameter set in its control system.

For this reason, grid operators may request that PV systems produce reactive energy to help compensate for the reactive power consumed by other elements connected elsewhere to the grid, such as motors or switching power supplies.